MyADOLC_NLP Class Reference

#include <Adolc_debugtest.h>

Inheritance diagram for MyADOLC_NLP:

Collaboration diagram for MyADOLC_NLP:

Public Member Functions
	MyADOLC_NLP ()
virtual	~MyADOLC_NLP ()
Overloaded from TNLP
virtual bool	get_nlp_info (Index &n, Index &m, Index &nnz_jac_g, Index &nnz_h_lag, IndexStyleEnum &index_style)
virtual bool	get_bounds_info (Index n, Number *x_l, Number *x_u, Index m, Number *g_l, Number *g_u)
virtual bool	get_starting_point (Index n, bool init_x, Number *x, bool init_z, Number *z_L, Number *z_U, Index m, bool init_lambda, Number *lambda)
template<class T >
bool	eval_obj (Index n, const T *x, T &obj_value)
template<class T >
bool	eval_constraints (Index n, const T *x, Index m, T *g)
virtual bool	eval_f (Index n, const Number *x, bool new_x, Number &obj_value)
virtual bool	eval_grad_f (Index n, const Number *x, bool new_x, Number *grad_f)
virtual bool	eval_g (Index n, const Number *x, bool new_x, Index m, Number *g)
virtual bool	eval_jac_g (Index n, const Number *x, bool new_x, Index m, Index nele_jac, Index *iRow, Index *jCol, Number *values)
virtual bool	eval_h (Index n, const Number *x, bool new_x, Number obj_factor, Index m, const Number *lambda, bool new_lambda, Index nele_hess, Index *iRow, Index *jCol, Number *values)
Solution Methods
virtual void	finalize_solution (SolverReturn status, Index n, const Number *x, const Number *z_L, const Number *z_U, Index m, const Number *g, const Number *lambda, Number obj_value, const IpoptData *ip_data, IpoptCalculatedQuantities *ip_cq)
virtual void	generate_tapes (Index n, Index m)

Methods to block default compiler methods.
The compiler automatically generates the following three methods. Since the default compiler implementation is generally not what you want (for all but the most simple classes), we usually put the declarations of these methods in the private section and never implement them. This prevents the compiler from implementing an incorrect "default" behavior without us knowing. (See Scott Meyers book, "Effective C++")
double **	Jac
double *	x_lam
double **	Hess
	MyADOLC_NLP (const MyADOLC_NLP &)
MyADOLC_NLP &	operator= (const MyADOLC_NLP &)

Detailed Description

Definition at line 37 of file Adolc_debugtest.h.

Constructor & Destructor Documentation

MyADOLC_NLP() [1/2]

MyADOLC_NLP

(

)

default constructor

Definition at line 34 of file Adolc_debugtest.cpp.

{}

~MyADOLC_NLP()

~MyADOLC_NLP ( )

virtual

default destructor

Definition at line 37 of file Adolc_debugtest.cpp.

{}

MyADOLC_NLP() [2/2]

MyADOLC_NLP ( const MyADOLC_NLP &  )

private

Member Function Documentation

eval_constraints()

template<class T >

bool eval_constraints	(	Index	n,
		const T *	x,
		Index	m,
		T *	g
	)

Template to compute contraints

Definition at line 116 of file Adolc_debugtest.cpp.

{
  for (Index i=0; i<m; i++) {
    g[i] = 3.*pow(x[i+1],3.) + 2.*x[i+2] - 5.
           + sin(x[i+1]-x[i+2])*sin(x[i+1]+x[i+2]) + 4.*x[i+1]
           - x[i]*exp(x[i]-x[i+1]) - 3.;
  }
 
  return true;
}

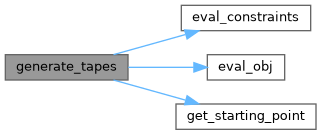
Referenced by eval_g(), and generate_tapes().

Here is the caller graph for this function:

eval_f()

bool eval_f ( Index  n, const Number *  x, bool  new_x, Number &  obj_value  )

virtual

Original method from Ipopt to return the objective value remains unchanged

Definition at line 136 of file Adolc_debugtest.cpp.

{
  eval_obj(n,x,obj_value);
 
  return true;
}

Here is the call graph for this function:

eval_g()

bool eval_g ( Index  n, const Number *  x, bool  new_x, Index  m, Number *  g  )

virtual

Original method from Ipopt to return the constraint residuals remains unchanged

Definition at line 151 of file Adolc_debugtest.cpp.

{
 
  eval_constraints(n,x,m,g);
 
  return true;
}

Here is the call graph for this function:

eval_grad_f()

bool eval_grad_f ( Index  n, const Number *  x, bool  new_x, Number *  grad_f  )

virtual

Original method from Ipopt to return the gradient of the objective remains unchanged

Definition at line 143 of file Adolc_debugtest.cpp.

{
 
  gradient(tag_f,n,x,grad_f);
 
  return true;
}

eval_h()

bool eval_h ( Index  n, const Number *  x, bool  new_x, Number  obj_factor, Index  m, const Number *  lambda, bool  new_lambda, Index  nele_hess, Index *  iRow, Index *  jCol, Number *  values  )

virtual

Original method from Ipopt to return: 1) The structure of the hessian of the lagrangian (if "values" is NULL) 2) The values of the hessian of the lagrangian (if "values" is not NULL) remains unchanged

Definition at line 190 of file Adolc_debugtest.cpp.

{
  if (values == NULL) {
    // return the structure. This is a symmetric matrix, fill the lower left
    // triangle only.
 
    // the hessian for this problem is actually dense
    Index idx=0;
    for (Index row = 0; row < n; row++) {
      for (Index col = 0; col <= row; col++) {
        iRow[idx] = row;
        jCol[idx] = col;
        idx++;
      }
    }
 
    assert(idx == nele_hess);
  }
  else {
    // return the values. This is a symmetric matrix, fill the lower left
    // triangle only
 
    for(Index i = 0; i<n ; i++)
      x_lam[i] = x[i];
    for(Index i = 0; i<m ; i++)
      x_lam[n+i] = lambda[i];
    x_lam[n+m] = obj_factor;
 
    hessian(tag_L,n+m+1,x_lam,Hess);
 
    Index idx = 0;
 
    for(Index i = 0; i<n ; i++)
      {
    for(Index j = 0; j<=i ; j++)
      {
        values[idx++] = Hess[i][j];
      }
      }
  }
 
  return true;
}

eval_jac_g()

bool eval_jac_g ( Index  n, const Number *  x, bool  new_x, Index  m, Index  nele_jac, Index *  iRow, Index *  jCol, Number *  values  )

virtual

Original method from Ipopt to return: 1) The structure of the jacobian (if "values" is NULL) 2) The values of the jacobian (if "values" is not NULL) remains unchanged

Definition at line 159 of file Adolc_debugtest.cpp.

{
  if (values == NULL) {
    // return the structure of the jacobian,
    // assuming that the Jacobian is dense
 
    Index idx = 0;
    for(Index i=0; i<m; i++)
      for(Index j=0; j<n; j++)
    {
      iRow[idx] = i;
      jCol[idx++] = j;
    }
 }
  else {
    // return the values of the jacobian of the constraints
 
    jacobian(tag_g,m,n,x,Jac);
 
    Index idx = 0;
    for(Index i=0; i<m; i++)
      for(Index j=0; j<n; j++)
      values[idx++] = Jac[i][j];
 
  }
 
  return true;
}

eval_obj()

template<class T >

bool eval_obj	(	Index	n,
		const T *	x,
		T &	obj_value
	)

Template to return the objective value

Definition at line 103 of file Adolc_debugtest.cpp.

{
  T a1, a2;
  obj_value = 0.;
  for (Index i=0; i<n-1; i++) {
    a1 = x[i]*x[i]-x[i+1];
    a2 = x[i] - 1.;
    obj_value += 100.*a1*a1 + a2*a2;
  }
 
  return true;
}

Referenced by eval_f(), and generate_tapes().

Here is the caller graph for this function:

finalize_solution()

void finalize_solution ( SolverReturn  status, Index  n, const Number *  x, const Number *  z_L, const Number *  z_U, Index  m, const Number *  g, const Number *  lambda, Number  obj_value, const IpoptData *  ip_data, IpoptCalculatedQuantities *  ip_cq  )

virtual

This method is called when the algorithm is complete so the TNLP can store/write the solution

Definition at line 237 of file Adolc_debugtest.cpp.

{
 
  printf("\n\nObjective value\n");
  printf("f(x*) = %e\n", obj_value);
 
// Memory deallocation for ADOL-C variables
 
  delete[] x_lam;
 
  for(Index i=0;i<m;i++)
    delete[] Jac[i];
  delete[] Jac;
 
  for(Index i=0;i<n+m+1;i++)
    delete[] Hess[i];
  delete[] Hess;
}

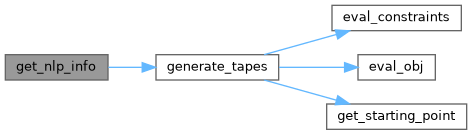
generate_tapes()

void generate_tapes ( Index  n, Index  m  )

virtual

Method to generate the required tapes

Definition at line 264 of file Adolc_debugtest.cpp.

{
  Number *xp    = new double[n];
  Number *lamp  = new double[m];
  Number *zl    = new double[m];
  Number *zu    = new double[m];
 
  adouble *xa   = new adouble[n];
  adouble *g    = new adouble[m];
  adouble *lam  = new adouble[m];
  adouble sig;
  adouble obj_value;
 
  double dummy;
 
  Jac = new double*[m];
  for(Index i=0;i<m;i++)
    Jac[i] = new double[n];
 
  x_lam   = new double[n+m+1];
 
  Hess = new double*[n+m+1];
  for(Index i=0;i<n+m+1;i++)
    Hess[i] = new double[i+1];
 
  get_starting_point(n, 1, xp, 0, zl, zu, m, 0, lamp);
 
  trace_on(tag_f);
 
    for(Index i=0;i<n;i++)
      xa[i] <<= xp[i];
 
    eval_obj(n,xa,obj_value);
 
    obj_value >>= dummy;
 
  trace_off();
 
  trace_on(tag_g);
 
    for(Index i=0;i<n;i++)
      xa[i] <<= xp[i];
 
    eval_constraints(n,xa,m,g);
 
 
    for(Index i=0;i<m;i++)
      g[i] >>= dummy;
 
  trace_off();
 
   trace_on(tag_L);
 
    for(Index i=0;i<n;i++)
      xa[i] <<= xp[i];
    for(Index i=0;i<m;i++)
      lam[i] <<= 1.0;
    sig <<= 1.0;
 
    eval_obj(n,xa,obj_value);
 
    obj_value *= sig;
    eval_constraints(n,xa,m,g);
 
    for(Index i=0;i<m;i++)
      obj_value += g[i]*lam[i];
 
    obj_value >>= dummy;
 
  trace_off();
 
  delete[] xa;
  delete[] xp;
  delete[] g;
  delete[] lam;
  delete[] lamp;
  delete[] zu;
  delete[] zl;
 
}

Referenced by get_nlp_info().

Here is the call graph for this function:

Here is the caller graph for this function:

get_bounds_info()

bool get_bounds_info ( Index  n, Number *  x_l, Number *  x_u, Index  m, Number *  g_l, Number *  g_u  )

virtual

Method to return the bounds for my problem

Definition at line 61 of file Adolc_debugtest.cpp.

{
  // none of the variables have bounds
  for (Index i=0; i<n; i++) {
    x_l[i] = -1e20;
    x_u[i] =  1e20;
  }
 
  // Set the bounds for the constraints
  for (Index i=0; i<m; i++) {
    g_l[i] = 0;
    g_u[i] = 0;
  }
 
  return true;
}

get_nlp_info()

bool get_nlp_info ( Index &  n, Index &  m, Index &  nnz_jac_g, Index &  nnz_h_lag, IndexStyleEnum &  index_style  )

virtual

Method to return some info about the nlp

Definition at line 39 of file Adolc_debugtest.cpp.

{
  n = 20;
 
  m = n-2;
 
  // in this example the jacobian is dense. Hence, it contains n*m nonzeros
  nnz_jac_g = n*m;
 
  // the hessian is also dense and has n*n total nonzeros, but we
  // only need the lower left corner (since it is symmetric)
  nnz_h_lag = n*(n-1)/2+n;
 
  generate_tapes(n, m);
 
  // use the C style indexing (0-based)
  index_style = C_STYLE;
 
  return true;
}

Here is the call graph for this function:

get_starting_point()

bool get_starting_point ( Index  n, bool  init_x, Number *  x, bool  init_z, Number *  z_L, Number *  z_U, Index  m, bool  init_lambda, Number *  lambda  )

virtual

Method to return the starting point for the algorithm

Definition at line 79 of file Adolc_debugtest.cpp.

{
  // Here, we assume we only have starting values for x, if you code
  // your own NLP, you can provide starting values for the others if
  // you wish.
  assert(init_x == true);
  assert(init_z == false);
  assert(init_lambda == false);
 
  // set the starting point
  for (Index i=0; i<n/2; i++) {
    x[2*i] = -1.2;
    x[2*i+1] = 1.;
  }
  if (n != 2*(n/2)) {
    x[n-1] = -1.2;
  }
 
  return true;
}

Referenced by generate_tapes().

Here is the caller graph for this function:

operator=()

MyADOLC_NLP & operator= ( const MyADOLC_NLP &  )

private

Member Data Documentation

Hess

double** Hess

private

Definition at line 141 of file Adolc_debugtest.h.

Referenced by eval_h(), finalize_solution(), and generate_tapes().

Jac

double** Jac

private

Definition at line 138 of file Adolc_debugtest.h.

Referenced by eval_jac_g(), finalize_solution(), and generate_tapes().

x_lam

double* x_lam

private

Definition at line 140 of file Adolc_debugtest.h.

Referenced by eval_h(), finalize_solution(), and generate_tapes().

---

The documentation for this class was generated from the following files:

• /exports/ffsm/src_latest/src/Adolc_debugtest.h
• /exports/ffsm/src_latest/src/Adolc_debugtest.cpp